FMPZ_POLY_Q Documentation

1.4.0

A FLINT-based implementation of the rational function field.

Overview

The module fmpz_poly_q provides functions for performing arithmetic on rational functions in 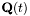, represented as quotients of integer polynomials of type fmpz_poly_t. These functions start with the prefix fmpz_poly_q_.

Rational functions are stored in objects of type fmpz_poly_q_t, which is an array of fmpz_poly_q_struct's of length one. This permits passing parameters of type fmpz_poly_q_t by reference. We also define the type fmpz_poly_q_ptr to be a pointer to fmpz_poly_q_struct's.

The representation of a rational function as the quotient of two integer polynomials can be made canonical by demanding the numerator and denominator to be coprime (as integer polynomials) and the denominator to have positive leading coefficient. As the only special case, we represent the zero function as 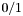. All arithmetic functions assume that the operands are in this canonical form, and canonicalize their result. If the numerator or denominator is modified individually, for example using the methods in the group Accessing numerator and denominator, it is the user's responsibility to canonicalize the rational function using the function fmpz_poly_q_canonicalize() if necessary.

All methods support aliasing of their inputs and outputs unless explicitly stated otherwise, subject to the following caveat. If different rational functions (as objects in memory, not necessarily in the mathematical sense) share some of the underlying integer polynomial objects, the behaviour is undefined.

The basic arithmetic operations, addition, subtraction and multiplication, are all implemented using adapted versions of Henrici's algorithms, see [H56]. Differentiation is implemented in a way slightly improving on the algorithm described in [H80].

Simple example

The following example computes the product of two rational functions and prints the result.

 #include "fmpz_poly_q.h"
 ...
 char *str, *strf, *strg;
 fmpz_poly_q_t f, g;
 fmpz_poly_q_init(f);
 fmpz_poly_q_init(g);
 fmpz_poly_q_from_string(f, "2  1 3/1  2");
 fmpz_poly_q_from_string(g, "1  3/2  2 7");
 strf = fmpz_poly_q_to_string_pretty(f, "t");
 strg = fmpz_poly_q_to_string_pretty(g, "t");
 fmpz_poly_q_mul(f, f, g);
 str  = fmpz_poly_q_to_string_pretty(f, "t");
 printf("%s * %s = %s\n", strf, strg, str);
 free(str);
 free(strf);
 free(strg);
 fmpz_poly_q_clear(f);
 fmpz_poly_q_clear(g);

The output is:

 (3*t+1)/2 * 3/(7*t+2) = (9*t+3)/(14*t+4)

Version history

• 1.4.0
  • Include fmpz_poly_q_print() and fmpz_poly_q_print_pretty()
  • Fix a bug in fmpz_poly_q_derivative() which leaves the derivative in a non-canonical form
  • Fix a bug in fmpz_poly_q_evaluate() which under-allocated a fmpz_t
  • Add various _randtest functions, which provide random (non-zero) rational functions, polynomials, and integers
  • Add lots of test code
• 1.3.0
  • Rename everything from qfmpz_poly_ to fmpz_poly_q_ in preparation for the integration into FLINT
  • Small change in the grouping of methods, to fit the better with other modules in FLINT or GMP
• 1.2.2
  • Rename _fmpz_evaluate_horner_mpq to _fmpz_poly_evaluate_mpq_horner, and remove the condition that the length of the polynomial must fit into a long rather than merely an unsigned long
  • Replacing exit statements with abort statements, since Sage apparently handles these better
• 1.2.1
  • Remove dependency on assert.h, replacing assertions by explicit checks followed by an error message and an exit statement
  • Small change to _fmpz_poly_q_sub_in_place()
  • Minor documentation changes
• 1.2.0
  • Henrici-like algorithm for qfmpz_poly_derivative()
  • Changed from fmpz_poly_t to fmpz_poly_p for the numerator and denominator
  • Direct access to the numerator and denominator
  • Increased code coverage through qfmpz_poly-test (qfmpz_poly.h 100%, qfmpz_poly.c 94.78%)
• 1.1.0
  • Minor bugfix in qfmpz_poly_evaluate()
• 1.0.0
  • First complete version

Bug:

The method fmpz_poly_q_to_string_pretty() leaks memory because the underlying FLINT 1.5.0 method does so.

Todo:

Implement some form of lazy evaluation. One strategy would be to change the representation of a rational function in the case of the zero function to NULL. This gives savings on initialization and checking whether a function is zero. Note that it is typically unlikely that an arithmetic operation on two functions yields zero, which is the only case in which this design choice yields extra work. Another approach would be to implement a delayed initialization of both the numerator and denominator. In either case, the methods providing direct access to the underlying polynomial objects would require more care.

See also:

[H56] - Peter Henrici, A Subroutine for Computations with Rational Numbers, J. ACM, 3, 1, 1956, 6-9, http://doi.acm.org/10.1145/320815.320818

[H80] - Ellis Horowitz, Algorithms for Rational Function Arithmetic Operations, Annual ACM Symposium on Theory of Computing: Proceedings of the Fourth Annual ACM Symposium on Theory of Computing (Denver), 108-118, 1972, http://doi.acm.org/10.1145/800152.804903