MONF Documentation

0.5

Author:: Sebastian Pancratz

Date:: Oct--Nov 2009

Acknowledgements:: I would like to thank Andrew Lewis from the Computer Laboratory at the University of Cambridge for helpful discussions.

Overview

The aim of this work is to provide a basic but very thin and fast implementation of monomials with only minimal overhead. The main step in order to achieve this is encoding a given monomial in one machine word, or possibly two, although this case is handled transparently. As a consequence of this design decision, this implementation can only be used for monomials in a fixed small number of variables and with small non-negative exponents.

Detailed introduction

We assume that a number $n+1$

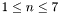of variables is fixed from the beginning, where $1 \leq n \leq 7$ , and that we only consider monomials with non-negative partial degrees of at most 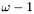$\omega - 1$ . Using 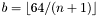$b = \lfloor{64/(n+1)}\rfloor$ bits per exponent, we can encode the monomial 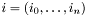$i = (i_0, \dotsc, i_n)$ as

$\sigma(i) = \sum_{j=0}^n i_j 2^{j b}$

in a 64-bit word as long as 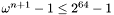$\omega^{n+1} - 1 \leq 2^{64} - 1$ . This allows us to handle the following exponent sizes:

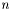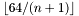	$\lfloor{64/(n+1)}\rfloor$	$\omega$
1	32	4294967296
2	21	2097152
3	16	65536
4	12	4096
5	10	1024
6	9	512
7	8	256

In order to define the degree with a unique signature for all of these values of 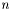$n$ , we assume that we only deal with monomials of degree less than 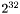$2^{32}$ . Note that this only affects the case $n = 1$ .

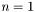It turns out that, for many operations on monomials, this form is very convenient in the sense that the operation can be performed on 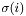$\sigma(i)$ as one word instead of 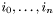$i_0, \dotsc, i_n$ involving $n+1$ words. Examples of this are multiplication and division, which correspond to addition and subtraction, and the inverse lexicographical order, which corresponds to the operator <. As an aside, the problem of possible overflow is burried in the our assumption that no monomial operation will involve partial exponents exceeding 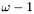$\omega - 1$ . Other operations, for example, checking whether one monomial is divisible by another, involve explicitly considering partial exponents using bitmasks.

Monomial orderings

The following (global) monomial orderings are typically considered:

Lexicographic ordering (lex).
$i < i' \iff \exists j \quad i_0 = i_0', \dotsc, i_{j-1} = i_{j-1}', i_j < i_j'$

Inverse lexicographic ordering (invlex).
$i < i' \iff \exists j \quad i_n = i_n', \dotsc, i_{j+1} = i_{j+1}', i_j < i_j'$

Degree lexicographic (deglex).
$i < i' \iff \deg(i) < \deg(i') \text{ or } \bigl(\deg(i) < \deg(i') \text{ and } \exists j \quad i_0 = i_0', \dotsc, i_{j-1} = i_{j-1}, i_j < i_j'\bigr)$

Degree reverse lexicographic (degrevlex).
$i < i' \iff \deg(i) < \deg(i') \text{ or } \bigl(\deg(i) < \deg(i') \text{ and } \exists j \quad i_n = i_n', \dotsc, i_{j+1} = i_{j+1}, i_j > i_j'\bigr)$

In this context, it is very useful to note that, in the inverse lexicographic ordering, we have 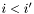$i < i'$ if and only 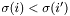$\sigma(i) < \sigma(i')$ . While the first test could involve $n+1$ word comparisons plus the overhead of a loop, the second test only involves one word comparison.