FMPQ_POLY Documentation

0.1.5

A FLINT-based implementation of the rational polynomial ring.

Overview

The module fmpq_poly provides functions for performing arithmetic on rational polynomials in , represented as quotients of integer polynomials of type fmpz_poly_t and denominators of type fmpz_t. These functions start with the prefix fmpq_poly_.

Rational polynomials are stored in objects of type fmpq_poly_t, which is an array of fmpq_poly_struct's of length one. This permits passing parameters of type fmpq_poly_t by reference. We also define the type fmpq_poly_ptr to be a pointer to fmpq_poly_struct's.

The representation of a rational polynomial as the quotient of an integer polynomial and an integer denominator can be made canonical by demanding the numerator and denominator to be coprime and the denominator to be positive. As the only special case, we represent the zero function as 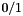. All arithmetic functions assume that the operands are in this canonical form, and canonicalize their result. If the numerator or denominator is modified individually, for example using the methods in the group Accessing numerator and denominator, it is the user's responsibility to canonicalize the rational function using the function fmpq_poly_canonicalize() if necessary.

All methods support aliasing of their inputs and outputs unless explicitly stated otherwise, subject to the following caveat. If different rational polynomials (as objects in memory, not necessarily in the mathematical sense) share some of the underlying integer polynomials or integers, the behaviour is undefined.

Version history

• 0.1.9
  • Add fmpq_poly_inv_series
  • Add fmpq_poly_div_series
  • Rename _fmpq_poly_from_list to fmpq_poly_from_list
  • Add static to the underscore methods
  • Remove the prefix and suffix _ in the header from _FMPQ_POLY_H_
  • Add fmpq_poly_print and fmpq_poly_print_pretty
• 0.1.8
  • Extra checks for NULL returns of malloc calls
• 0.1.7
  • Explicit casts for return values of malloc
  • Changed a few calls to GMP and FLINT methods from _si to _ui
• 0.1.6
  • Added tons of testing code in the subdirectory test
  • Made a few changes throughout the code base indicated by the tests
• 0.1.5
  • Re-wrote the entire code to always initialise the denominator
• 0.1.4
  • Fixed a bug in fmpq_poly_divrem()
  • Swapped calls to fmpq_poly_degree to calls to fmpq_poly_length in many places
• 0.1.3
  • Changed fmpq_poly_inv()
  • Another sign check to fmpz_abs in fmpq_poly_content()
• 0.1.2
  • Introduce a function fmpq_poly_monic() and use this to simplify the code for the gcd and xgcd functions
  • Make further use of fmpq_poly_is_zero()
• 0.1.1
  • Replaced a few sign checks and negations by fmpz_abs
  • Small changes to comments and the documentation
  • Moved some function bodies from fmpq_poly.h to fmpq_poly.c
• 0.1.0
  • First draft, based on the author's Sage code